Lab 1 - Wprowadzenie do Robotics Toolbox for Python
Modelowanie i sterowanie robotów - laboratorium
Lab 1 - Wprowadzenie do Robotics Toolbox for Python
Politechnika Poznańska
Instytut Robotyki i Inteligencji Maszynowej

Jakub Chudziński, Bartłomiej Kulecki
Wstęp
W pierwszej części zajęć laboratoryjnych z Modelowania i Sterowania Robotów pracować będziemy z biblioteką Spatialmath oraz Robotics Toolbox. Będziemy wykorzystywać język Python 3 - w przypadku konieczności przypomnienia sobie procedury instalacji i konfiguracji środowiska, a także podstawowego użycia pakietów (np. numpy) można sięgnąć do tutoriali z przedmiotu Technologie Informacyjne (instrukcje 05a, 05b, 06).
Robotics Toolbox (RTB) jest biblioteką dla języka Python 3, która stanowi odpowiednik pierwotnej wersji Robotics Toolbox dla środowiska MATLAB. Autorem obu wersji jest Peter Corke.
RTB zapewnia narzędzia do reprezentacji kinematyki i dynamiki manipulatorów o złączach połączonych szeregowo (czyli w formie łańcuchów kinematycznych) - umożliwia tworzenie własnych w formie notacji Denavita-Hartenberga, zaimportowanie pliku URDF lub użycie ponad 30 dostarczonych modeli dla znanych współczesnych robotów firmy Franka-Emika, Kinova, Universal Robotics, Rethink, a także klasycznych robotów, takich jak Puma 560 i ramię Stanford. Toolbox pozwala na modelowanie, wizualizację i symulację ruchu robotów.
Dokumentację Robotics Toolbox można znaleźć pod
adresami:
https://petercorke.github.io/robotics-toolbox-python/index.html
https://github.com/petercorke/robotics-toolbox-python
https://github.com/petercorke/robotics-toolbox-python/wiki
Przygotowanie środowiska pracy
Instalacja (Windows)
Na komputerach w laboratorium można pominąć proces instalacji.
Jednak rekomendowana jest instalacja potrzebnego oprogramowania na własnym komputerze, instrukcja
Tworzenie projektu
Utwórz nowy projekt w wybranym IDE:
- PyCharm instrukcja
- Visual Studio Code instrukcja
Szablon kodu
Można skorzystać z następującego szablonu pliku .py:
# wczytanie potrzebnych podczas zajęć bibliotek:
import roboticstoolbox as rtb
import numpy as np
from spatialmath import *
from spatialmath.base import *
from spatialmath.base.symbolic import *
from matplotlib import pyplot as plt
# ...
# definicje funkcji:
def przyklad_1():
pass # zastąp tę linię swoim kodem
def zadanie_1():
pass # zastąp tę linię swoim kodem
def zadanie_2():
pass # zastąp tę linię swoim kodem
# ...
# wykonywanie wybranej funkcji
if __name__ == '__main__':
przyklad_1()Biblioteka Spatialmath
Dostępne klasy
Podstawą robotyki i wizji komputerowej są metody opisu położenia/pozy
(czyli pozycji i orientacji) obiektów w przestrzeni 2D lub 3D.
Biblioteka spatialmath oferuje różne klasy do reprezentacji
pozycji i orientacji w przestrzeni:
| reprezentacja | w 3D | w 2D |
|---|---|---|
| położenie (pozycja+orientacja) | SE3, Twist3,
UnitDualQuaternion |
SE2, Twist2 |
| orientacja | SO3, UnitQuaternion |
SO2 |
SE3- macierz należąca do grupy SE(3), opisuje pozycję i orientację w 3 wymiarach,SE2- macierz należąca do grupy SE(2), opisuje pozycję i orientację w 2 wymiarach,SO3- macierz należąca do grupy SO(3), opisuje orientację w 3 wymiarach,SO2- macierz należąca do grupy SO(2), opisuje orientację w 2 wymiarach,UnitQuaternion- kwaternion należący do grupy S3, opisuje orientację w 3 wymiarach,UnitDualQuaternion- podwójny kwaternion rzutowany do grupy SE(3), opisuje pozycję i orientację (położenie) w 3 wymiarach,Twist3- wektor należący do grupy SE(3), opisuje położenie w 3 wymiarach,Twist2- wektor należący do grupy SE(2), opisuje położenie w 2 wymiarach.
W kategoriach matematycznych położenie stanowi grupę - SE(3) oznacza specjalną grupę euklidesową w 3 wymiarach (w praktyce jest to znana nam reprezentacja - macierz transformacji 4x4), a SE(2) oznacza specjalną grupę euklidesową w 2 wymiarach (macierz transformacji 3x3). Orientacja jest reprezentowana jako SO(3) lub SO(2) - specjalna grupa ortogonalna w 3 lub 2 wymiarach (jest to macierz rotacji 3x3 lub 2x2).
Dla przykładu, możemy zdefiniować macierz rotacji opisującą obrót wokół osi x o 0.3 radiana:
R1 = SO3.Rx(0.3)
print(R1)
1 0 0
0 0.9553 -0.2955
0 0.2955 0.9553 Gdy pozostawimy konstruktor bez argumentu otrzymamy macierz jednostkową, która odpowiada zerowej rotacji. Można również podawać kąty w stopniach, np. rotacja wokół osi z o 30 stopni:
R2 = SO3.Rz(30, 'deg')
print(R2)
0.866 -0.5 0
0.5 0.866 0
0 0 1 Złożenie tych dwóch rotacji polega na pomnożeniu obu macierzy:
R = R1 * R2
print(R)
0.866 -0.5 0
0.4777 0.8273 -0.2955
0.1478 0.2559 0.9553 Można także “ręcznie” utworzyć całą macierz rotacji, np.:
Rot = SO3(np.array([[-1, 0, 0],
[ 0, 1, 0],
[ 0, 0, -1]]))
print(Rot)Często w robotyce potrzebna jest sekwencja orientacji, z których składa się trajektoria. Aby stworzyć listę macierzy rotacji, wystarczy podać jako argument konstruktora listę kątów zamiast pojedynczej wartości.
Zadanie:
Korzystając z funkcji biblioteki numpy stwórz listę 30 macierzy rotacji wokół osi x, dla 30 kątów w zakresie od \(0\) do \(2\pi\).Podpowiedź
Skorzystaj z funkcji:np.linspace
Klasa SE3 pozwala na zdefiniowanie macierzy
transformacji 4x4. Przykładowo, aby uzyskać macierz transformacji z
zerową rotacją i niezerową translacją, należy wpisać:
T1 = SE3(0.5, 1.0, 0.1) # Macierz transformacji zawierająca tylko translację
print(T1)
1 0 0 0.5
0 1 0 1
0 0 1 0.1
0 0 0 1Obrót wokół jednej osi i złożenie dwóch transformacji:
T2 = SE3.Ry(45, 'deg') # Macierz transformacji zawierająca tylko rotację
T = T1 * T2 # Złożenie obu macierzy (translacja i rotacja)
print(T)
0.7071 0 0.7071 0.5
0 1 0 1
-0.7071 0 0.7071 0.1
0 0 0 1 Metoda SE3.Rt(R,t) umożliwiająca utworzenie macierzy
transformacji na podstawie zadanej rotacji R i translacji
t:
Rot = SO3.Ry(45, 'deg') # Macierz rotacji typu SO3 (lub numpy array o rozmiarze 3x3)
Pos = np.array([0.5, 1, 0.1]) # Wektor translacji o rozmiarze 1x3
T = SE3.Rt(Rot,Pos)
print(T)
0.7071 0 0.7071 0.5
0 1 0 1
-0.7071 0 0.7071 0.1
0 0 0 1 Macierz transformacji SE(3) można uzyskać przechodząc od różnych reprezentacji rotacji. Konwersje można wykonywać pomiędzy takimi reprezentacjami jak np. kąty roll, pitch, yaw, kąty Eulera, notacja oś-kąt, kwaterniony. Przykładowe funkcje:
T = SE3(1,2,3)
# odwrotność
print( T.inv() )
1 0 0 -1
0 1 0 -2
0 0 1 -3
0 0 0 1
# sprawdzenie czy macierz T należy do SE(3)
print( T.isvalid(T.A) )
True
# kąty roll, pitch, yaw -> macierz transformacji 4x4
T1 = SE3.RPY([0.1, 0.2, 0.3], order='xyz')
# rotacja wokół osi -> kwaternion
q = UnitQuaternion.Rx(0.3)
print(q)
0.9888 << 0.1494, 0.0000, 0.0000 >>Klasy vs. funkcje niższego poziomu
Korzystanie z klas przedstawionych powyżej niesie za sobą następujące korzyści (które generalnie wynikają ze stosowania klas):
- bezpieczeństwo typów - nie jest możliwe połączenie macierzy rotacji 3D z ruchem sztywnego ciała 2D, mimo że oba są reprezentowane przez macierz 3×3,
- przeciążanie operatorów pozwala na wygodne i czytelne wyrażanie algorytmów,
- klasy mogą reprezentować nie tylko pojedynczą wartość, ale sekwencję wartości, które są obsługiwane przez operatory z niejawnym nadawaniem wartości.
Objaśnienie tych zalet znaleźć można także tutaj.
Istnieje jednak możliwość korzystania z funkcji
niższego poziomu z pominięciem warstwy abstrakcji, jaką są klasy.
Funkcje te są dostępne w bibliotece spatialmath.base (dokumentacja)
i są odpowiednikami funkcji, które były dostępne w wersji Robotics
Toolbox dla MATLABa.
Korzystając z klas możemy (a w pewnych sytuacjach wręcz potrzebujemy)
dostać się do “surowych” danych naszej macierzy. W tym celu można
odwołać się do atrybutów klasy SE3 lub SO3,
np.:
T = SE3(1,2,3)*SE3.Rx(np.pi/2.0)
print('Cała macierz transformacji:')
print(T.A)
print('Macierz rotacji:')
print(T.R)
print('Wektor translacji:')
print(T.t)
# sprawdzenie typu zmiennej:
print(type(T.A))
<class 'numpy.ndarray'>Wszystkie te atrybuty to dwuwymiarowe tablice
numpy.ndarray. Aby je pomnożyć, należy skorzystać z
operatora @, np.
T1 = SE3(1,2,3)*SE3.Rx(np.pi/2.0)
T2 = SE3(0,0,1)
T_SE = T1 * T2
T_np = T1.A @ T2.AWykresy
Biblioteka spatialmath pozwala również na wyświetlanie
układów współrzędnych (jednego lub wielu) na wykresie. Przykład:
# złożenie trzech przekształceń (translacja, rotacja o kąty RPY, rotacja wokół osi x)
T = SE3(0.5, 0.0, 0.0) * SE3.RPY([0.1, 0.2, 0.3], order='xyz') * SE3.Rx(-90, unit='deg')
print(T)
T1 = SE3(1,2,3)
T2 = SE3(3,1,2)
T.plot(frame='A', style='rviz', width=2)
T1.plot(frame='B', color='red', width=3)
T2.plot(frame='C', color='green', width=1)
plt.show()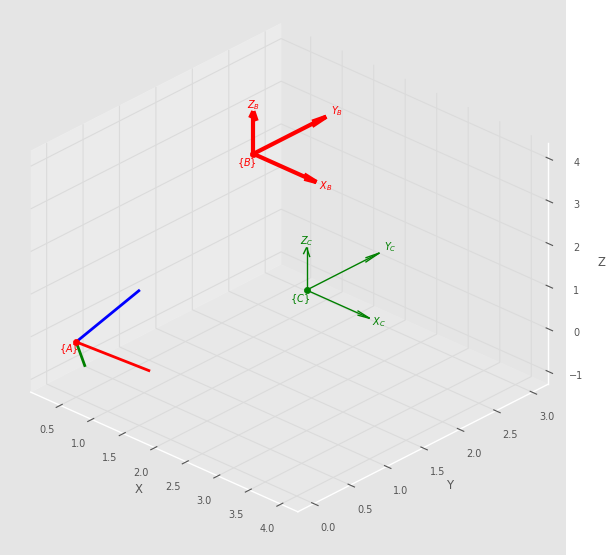
Jeśli układy nie pokazują się w jednym oknie, zainstaluj starszą wersję biblioteki matplotlib, korzystając z komendy:
pip install matplotlib==3.6.3
Poza prezentacją układów na wykresie istnieje możliwość stworzenia animacji przedstawiającej transformację układu do danej pozycji.
T = SE3(3, 1, 2) * SE3.RPY(0.1, 0.2, 0.3, order='xyz') * SE3.Rx(-90, 'deg')
T.animate(frame='A', color='red', width=2, dims=[0, 3], nframes=100)
plt.show()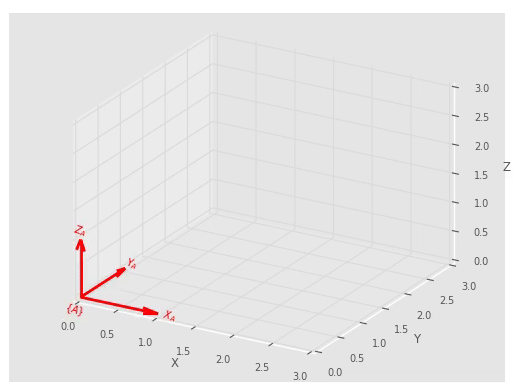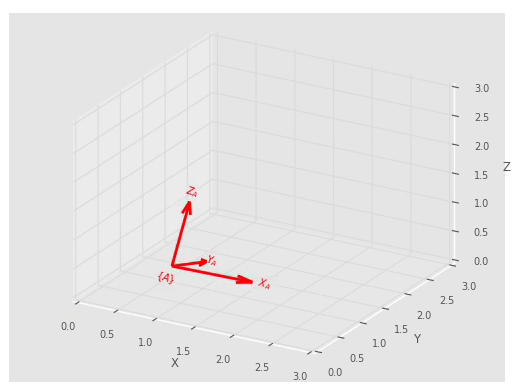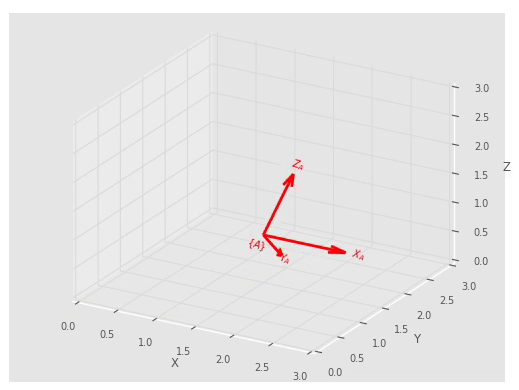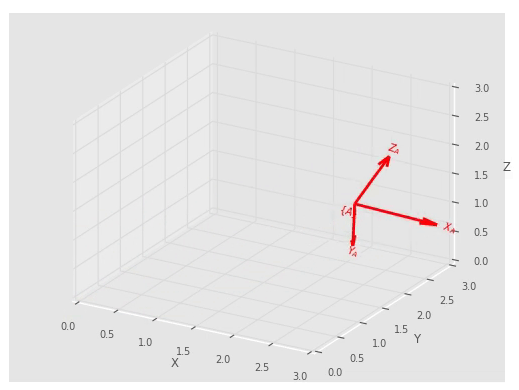
Zmienne symboliczne
Dzięki wykorzystaniu sympy, biblioteka
spatialmath oferuje także możliwość stosowania zmiennych
symbolicznych i wykonywania na nich operacji za pomocą standardowo
dostępnych funkcji.
Przykładowe definicje zmiennych symbolicznych:
# wymagany import biblioteki:
# from spatialmath.base.symbolic import *
alpha = symbol('alpha')
print(alpha)
alpha
phi, theta, psi = symbol('phi, theta, psi')
q = symbol('q_:6')
print(q)
(q_0, q_1, q_2, q_3, q_4, q_5)Inne przykładowe funkcje:
# funkcje trygonometryczne
print(cos(phi))
cos(phi)
print(cos(3.14))
-0.9999987317275395
# symboliczna liczba pi
print(sin(pi()))
0
print(sin(np.pi))
1.2246467991473532e-16
# sprawdzenie czy zmiennna jest symboliczna
print( issymbol(theta) )
True
print( issymbol(3.5) )
False
# pierwiastek
x = symbol('x')
print(sqrt(x**2))
Abs(x)
print(sqrt(4))
2.0
# upraszczanie wyrażenia
y = (x - 1) * (x + 1) - x ** 2
print(y)
-x ** 2 + (x - 1) * (x + 1)
print(simplify(y))
-1🔥 💥 Zadania do wykonania: 💥 🔥
Zadanie 1.
Korzystając z klasy SO3 utwórz macierz rotacji:
\[R_{3}^{0}=R_{Z}(-\pi / 3) R_{Y}(\pi / 6)
R_{X}(-\pi / 4)\]
SO3 utwórz macierz rotacji:M = SO3.Rz(-np.pi/3.0) * SO3.Ry(np.pi/6.0) * SO3.Rx(-np.pi/4.0)Podaj dwie interpretacje tak utworzonej macierzy z punktu widzenia osi, wokół których realizowane są obroty składowe i kolejność ich realizacji.
Powyższa sekwencja obrotów ZYX może być interpretowana w dwa ekwiwalentne sposoby. Po pierwsze, korzystając z mnożenia lewostronnego (pre-multiplication, extrinsic rotation), możemy rozpatrywać od prawej strony do lewej jako obroty wokół stałego układu odniesienia. Po drugie, od lewej do prawej, jako obroty wokół osi nowego układu odniesienia (post-multiplication, intrinsic rotations).Poniżej przedstawiono wizualizację dwóch tożsamych interpretacji rotacji: \[R_{3}^{0}=R_{Z}(\pi / 2) R_{Y}(\pi / 4) R_{X}(\pi )\]
 |
 |
|---|---|
| Yaw-Pitch’-Roll’’ (intrinsic rotation) | Roll-Pitch-Yaw (extrinsic rotation) |
Wizualizacje zaczerpnięto z podanego odnośnika.
Które z podanych kątów to wartości Roll, Pitch, Yaw?
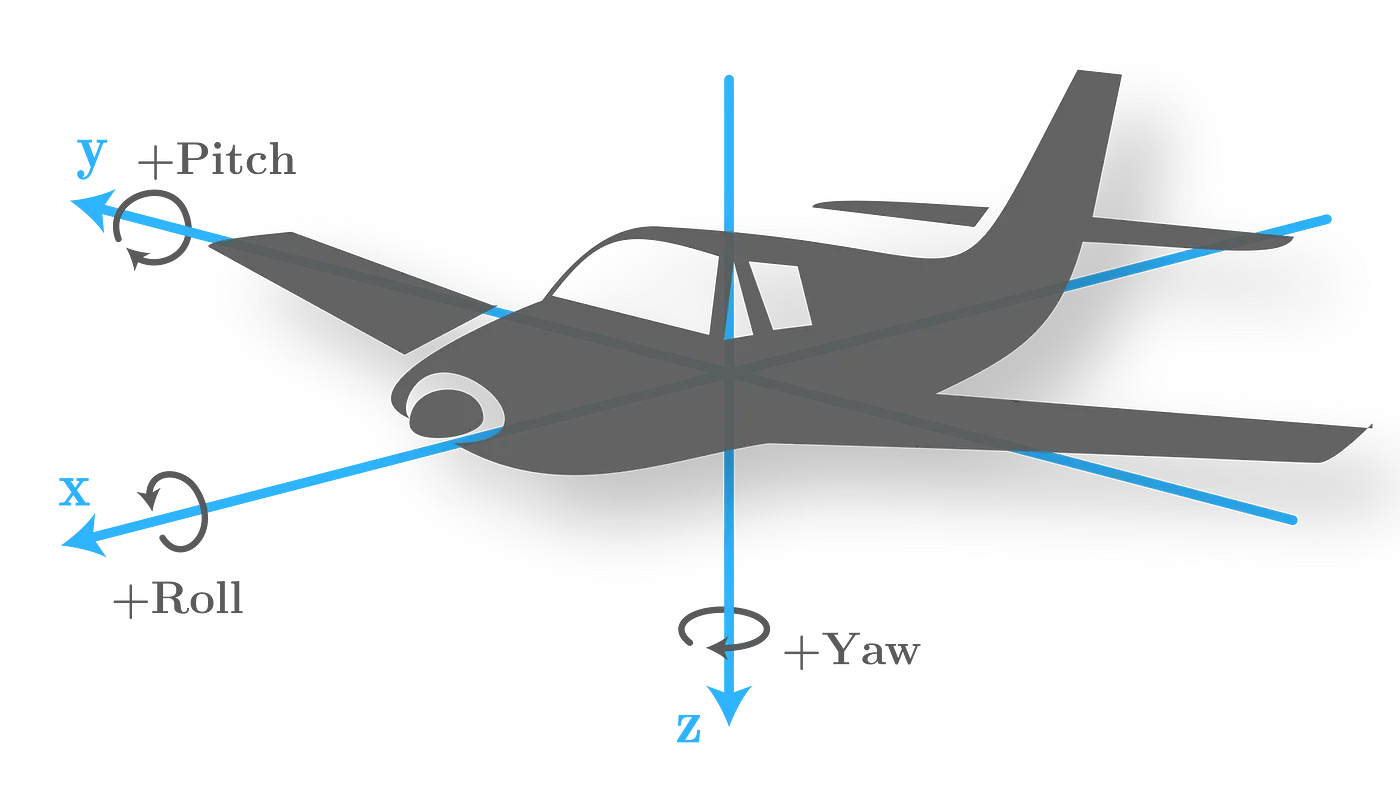
Roll = \(-\pi / 4\), Pitch = \(\pi / 6\), Yaw = \(-\pi / 3\)
Wyznacz kąty Eulera na podstawie macierzy. Sprawdź w dokumentacji, jakich osi dotyczą uzyskane kąty. Zdefiniuj macierz rotacji od nowa na podstawie otrzymanych kątów Eulera.
M = SO3.Rz(-np.pi/3.0) * SO3.Ry(np.pi/6.0) * SO3.Rx(-np.pi/4.0)
print(M)
e1, e2, e3 = M.eul()
print("Euler angles: ", M.eul(unit='deg'))
M = SO3.Eul([e1, e2, e3])
print(M)Stwórz animację przedstawiającą rotację układu współrzędnych za pomocą otrzymanej macierzy rotacji \(R_3^0\).
Na przykładzie macierzy \(R_3^0\) numerycznie sprawdź następujące własności macierzy rotacji (wyświetl i porównaj wyniki):
- \(det(R) = 1\)
- \(R^{-1} = R^T\)
- \(n^To = o^Ta = a^Tn = 0\)
- \(||n||=||o||=||a|| = 1\)
- \(n\times o=a, \;\;\; o\times a=n, \;\;\; a\times n=o\)
gdzie \(R =\left[\begin{array}{lll} n & o & a\end{array}\right]\).
💡 Skorzystaj z funkcji biblioteki
numpy(import numpy as np):np.linalg.det,np.transpose,np.linalg.inv, operatora mnożenia@,np.linalg.norm,np.cross
Zadanie 2.
Przypomnijmy sobie zadania z notacji Denavita-Hartenberga (standardowej) rozwiązywane podczas ćwiczeń z Podstaw Robotyki. Oto jedno z nich:
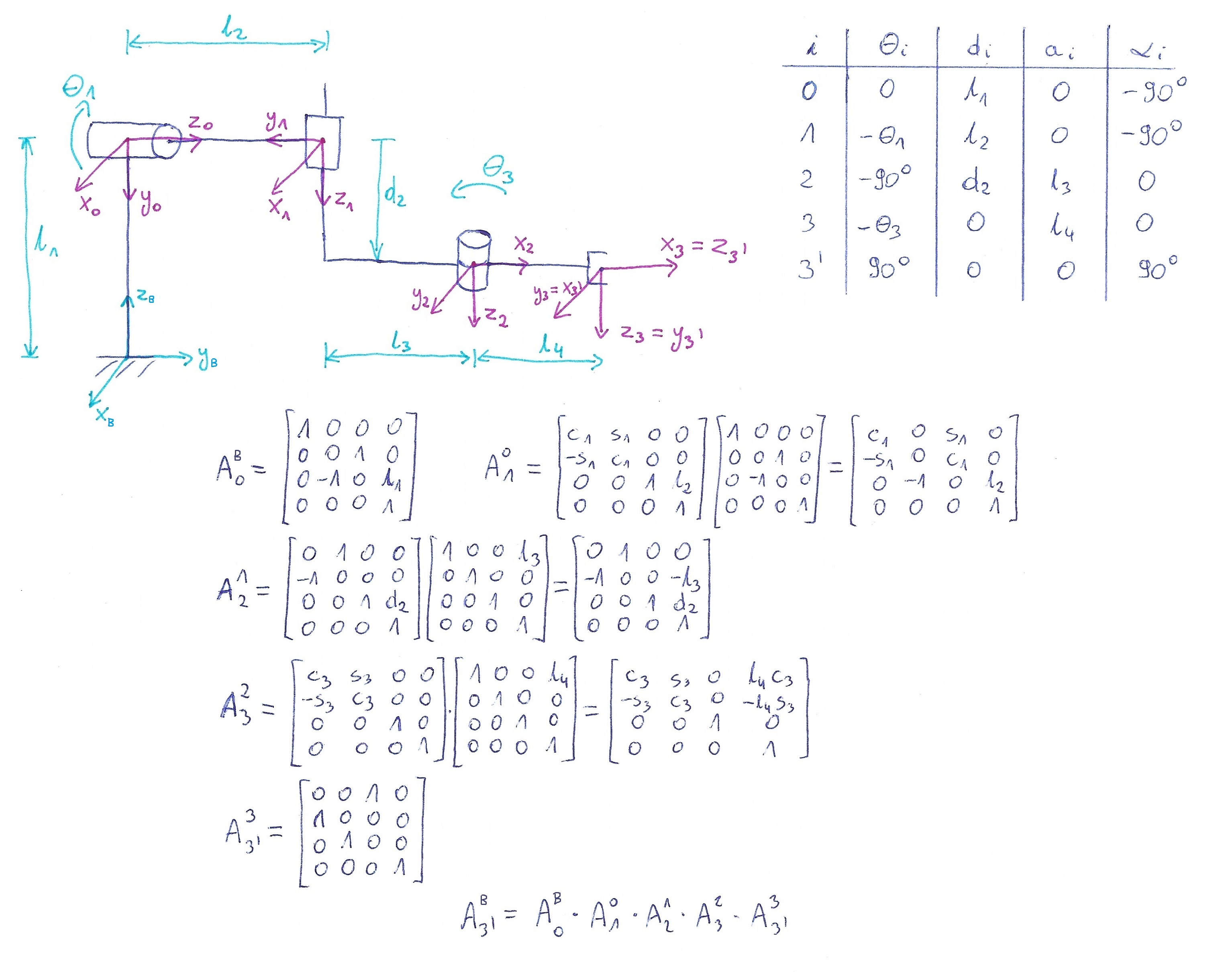
Za pomocą poznanej klasy SE3 i jej metod wyznacz (na
podstawie tabeli DH) macierze \(A_0^B\), \(A_1^0\), \(A_2^1\),
\(A_3^2\), \(A_{3’}^3\) oraz macierz \(A_{3’}^B\) (układ B to układ
bazowy - globalny, natomiast układ 0 to układ zerowy robota, układ 3’ to
układ końcówki roboczej). Wykorzystaj zmienne symboliczne, wartości
liczbowe (wartości zerowe) i kąty +/-90. Sprawdź, czy otrzymane wyniki
zgadzają się z tymi zaprezentowanymi na obrazie.
Notacja \(A_b^a\) oznacza macierz transformacji od układu a do b (wyraża pozycję układu b względem a).
💡 Gdy podamy kąty w radianach, macierze po wyświetleniu będą bardziej czytelne. Kąty +/-90 możesz zdefiniować korzystając z metody
pi()zespatialmath.base.symbolic💡
Do wyświetlania macierzy zawierającej zmienne symboliczne, możesz
wykorzystać poniższą funkcję (zamiast zwykłej funkcji
print):
def print_SE3(SE3_matrix : SE3):
SE3_numpy = SE3_matrix.A
max_item_length = SE3_numpy.astype(np.string_).dtype.itemsize
with np.printoptions(precision=3, suppress=True, linewidth = np.inf, formatter = {'all':lambda x: f"{str(x):{max_item_length}}"}):
print(SE3_numpy)Zadanie 3.
Przypomnienie:
Transformacje jednorodne umożliwiają jednoznaczny i zwarty opis zarówno pozycji jak i orientacji układu współrzędnych \(\{B\}\) względem układu \(\{A\}\) za pomocą następującej macierzy: \[ T_{B}^{A} =\left[\begin{array}{cc}R_{B}^{A} & t_{B}^{A} \\ 0_{1 \times 3} & 1\end{array}\right] \in SE(3)\] gdzie \(R_B^A\) jest macierzą rotacji reprezentującą orientacje osi układu \(\{B\}\) względem układu \(\{A\}\), zaś wektor \[t_B^A = \left[\begin{array}{lll}t_{Bx} & t_{By} & t_{Bz}\end{array}\right]^{T}\] reprezentuje pozycję początku układu \(\{B\}\) względem początku układu \(\{A\}\).
Przekształcenie punktu \(D^B\), reprezentowanego we współrzędnych jednorodnych wektorem \[ \underline{d}^{B}=\left[\left(d^{B}\right)^{T} \\; 1\right]^{T}=\left[\begin{array}{lll}d_{x} & d_{y} & d_{z} & 1\end{array}\right]^{T} \] do układu \(\{A\}\) wynika teraz z następującej operacji: \[ \underline{d}^{A}=T_{B}^{A} \underline{d}^{B} \Rightarrow d^{A}=R_{B}^{A} d^{B}+t_{B}^{A} \] Transformacja odwrotna, która reprezentuje orientacje osi i pozycję początku układu \(\{A\}\) względem układu \(\{B\}\) określona jest w następujący sposób: \[ T_{A}^{B}=\left(T_{B}^{A}\right)^{-1}=\left[\begin{array}{cc} \left(R_{B}^{A}\right)^{T} & -\left(R_{B}^{A}\right)^{T} t_{B}^{A} \\ 0_{1 \times 3} & 1 \end{array}\right] \in SE(3) \]
Zadanie 3.1.
Dane są trzy układy współrzędnych: \(\{B\}\), \(\{S\}\), \(\{P\}\), oraz dany jest punkt \(D\) reprezentowany przez wektor \(d^P\) wyrażony względem układu współrzędnych \(\{P\}\) jako: \[ d^{P} =\left[\begin{array}{r} 1 \\ -2 \\ 2 \end{array}\right] \]
Relacje między poszczególnymi układami współrzędnych definiują następujące wektory i macierze:
\[ t_{S}^{B} =\left[\begin{array}{l} 2 \\ 5 \\ 0 \end{array}\right], \quad t_{S}^{P} =\left[\begin{array}{r} 3 \\ -6 \\ 4 \end{array}\right], \quad R_{S}^{B} =\left[\begin{array}{rrr} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right], \quad R_{S}^{P} =\left[\begin{array}{rrr} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{array}\right] \]
gdzie \(t\) jest wektorem łączącym początki odpowiednich układów.
Stosując formalizm transformacji jednorodnych oblicz współrzędne wektora
\(d^B\) (współrzędne punktu \(D\) w układzie \(\{B\}\) ).
Skorzystaj z klas biblioteki spatialmath: SO3, SE3 a także
numpy array.
Prawidłowa odpowiedź:
[ -2 7 2 ]
Zadanie 3.2.
Korzystając z metody plot stwórz jeden wykres
przedstawiający wszystkie 3 układy współrzędnych (układ \(\{B\}\)
potraktować jako układ globalny). Dodaj do wykresu wektor (strzałkę)
funkcją plt.quiver, który będzie odpowiadał wektorowi
\(d^B\) i zweryfikuj poprawność pozycji punktu \(D\) (końcówki strzałki)
względem układu \(\{P\}\).
Pamiętaj o funkcji
plt.show()
Zadanie domowe
W ramach lab nr 1 należy rozwiązać zadanie domowe (zadanie 3.1 i 3.2 z instrukcji) na eKursie (ma ono formę zadania testowego w CodeRunnerze). Czas na wykonanie jest wyświetlony w module zadania na eKursie.