Lab 2 - Modelowanie manipulatorów w RT - kinematyka prosta i odwrotna
Modelowanie i sterowanie robotów - laboratorium
Lab 2 - Modelowanie manipulatorów w RT - kinematyka prosta i odwrotna
Politechnika Poznańska
Instytut Robotyki i Inteligencji Maszynowej

Jakub Chudziński, Bartłomiej Kulecki
Szablon kodu
Otwórz swój istniejący lub utwórz nowy projekt w wybranym IDE:
- PyCharm instrukcja
- Visual Studio Code instrukcja
Można skorzystać z następującego szablonu pliku .py:
# wczytanie potrzebnych podczas zajęć bibliotek:
import roboticstoolbox as rtb
import numpy as np
import math
from spatialmath import *
from spatialmath.base import *
from spatialmath.base.symbolic import *
import time
# ...
# definicje funkcji:
def przyklad_1():
pass # zastąp tę linię swoim kodem
def zadanie_1():
robot = None # zastąp tę linię swoim kodem
return robot
def zadanie_2(robot):
pass # zastąp tę linię swoim kodem
def zadanie_3(robot):
pass # zastąp tę linię swoim kodem
def zadanie_4():
pass # zastąp tę linię swoim kodem
def zadanie_5():
pass # zastąp tę linię swoim kodem
# ...
# wykonywanie wybranej funkcji
if __name__ == '__main__':
przyklad_1()
#robot = zadanie_1()
#zadanie_2(robot)
#zadanie_3(robot)
#zadanie_4()
#zadanie_5()Wstęp
W ramach Robotics Toolbox dostępnych jest ponad 30 gotowych modeli robotów. Niektóre z nich, poza zdefiniowaną strukturą kinematyczną, posiadają także parametry bezwładności i tarcia. Modele kinematyczne można zdefiniować na różne sposoby:
- standardową lub zmodyfikowaną notacją Denavita-Hartenberga (DH lub MDH),
- jako łańcuch ETS (Elementary Transformations Sequence),
- jako drzewo brył sztywnych,
- w formie pliku URDF (Unified Robot Description Format).
Listę dostępnych modeli można podejrzeć korzystając z podpowiedzi IDE wyświetlanych po wpisaniu:
rtb.models.
# lub
rtb.models.DH.
# lub
rtb.models.ETS. Klasa DHRobot
Do definicji kinematycznego modelu robota w notacji
Denavita-Hartenberga służy klasa DHRobot. Aby stworzyć
model manipulatora, należy przekazać do konstruktora klasy listę
obiektów typu DHLink, zawierającą parametry poszczególnych
ogniw i współrzędne konfiguracyjne węzłów (\(\theta\), \(d\), \(a\), \(\alpha\)). Należy również określić rodzaj
połączenia, dla obrotowego są to podklasy RevoluteDH i
RevoluteMDH, a dla przesuwnego PrismaticDH i
PrismaticMDH. Za pomocą innych argumentów konstruktora -
słów kluczowych - można także zdefiniować takie parametry jak masa,
pozycja środka masy, inercja, tarcie czy też limity przegubów.
Przykład:
robot = rtb.DHRobot(
[
rtb.RevoluteDH(alpha= np.pi / 2),
rtb.RevoluteDH(a=0.4318),
rtb.RevoluteDH(d=0.15005, a=0.0203, alpha= -np.pi / 2),
rtb.RevoluteDH(d=0.4318, alpha= np.pi / 2),
rtb.RevoluteDH(alpha= -np.pi / 2),
rtb.RevoluteDH()
], name="My_Robot")
print(robot)
┏━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━┓
┃θⱼ ┃ dⱼ ┃ aⱼ ┃ ⍺ⱼ ┃
┣━━━━╋━━━━━━━━━╋━━━━━━━━╋━━━━━━━━┫
┃ q1 ┃ 0.0 ┃ 0.0 ┃ 90.0° ┃
┃ q2 ┃ 0.0 ┃ 0.4318 ┃ 0.0° ┃
┃ q3 ┃ 0.15 ┃ 0.0203 ┃ -90.0° ┃
┃ q4 ┃ 0.4318 ┃ 0.0 ┃ 90.0° ┃
┃ q5 ┃ 0.0 ┃ 0.0 ┃ -90.0° ┃
┃ q6 ┃ 0.0 ┃ 0.0 ┃ 0.0° ┃
┗━━━━┻━━━━━━━━━┻━━━━━━━━┻━━━━━━━━┛Opis struktury kinematycznej robota wczytanego z dostępnej puli modeli można wyświetlić w następujący sposób:
robot = rtb.models.DH.Puma560()
print(robot)
┏━━━━┳━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┓
┃θⱼ ┃ dⱼ ┃ aⱼ ┃ ⍺ⱼ ┃ q⁻ ┃ q⁺ ┃
┣━━━━╋━━━━━━━━━━━━━━━━━━━━╋━━━━━━━━╋━━━━━━━━╋━━━━━━━━━╋━━━━━━━━┫
┃ q1 ┃ 0.6718 ┃ 0 ┃ 90.0° ┃ -160.0° ┃ 160.0° ┃
┃ q2 ┃ 0 ┃ 0.4318 ┃ 0.0° ┃ -110.0° ┃ 110.0° ┃
┃ q3 ┃ 0.15 ┃ 0.0203 ┃ -90.0° ┃ -135.0° ┃ 135.0° ┃
┃ q4 ┃ 0.4318 ┃ 0 ┃ 90.0° ┃ -266.0° ┃ 266.0° ┃
┃ q5 ┃ 0 ┃ 0 ┃ -90.0° ┃ -100.0° ┃ 100.0° ┃
┃ q6 ┃ 0 ┃ 0 ┃ 0.0° ┃ -266.0° ┃ 266.0° ┃
┗━━━━┻━━━━━━━━━━━━━━━━━━━━┻━━━━━━━━┻━━━━━━━━┻━━━━━━━━━┻━━━━━━━━┛
┌─────┬─────┬──────┬───────┬─────┬──────┬─────┐
│name │ q0 │ q1 │ q2 │ q3 │ q4 │ q5 │
├─────┼─────┼──────┼───────┼─────┼──────┼─────┤
│ qz │ 0° │ 0° │ 0° │ 0° │ 0° │ 0° │
│ qr │ 0° │ 90° │ -90° │ 0° │ 0° │ 0° │
│ qs │ 0° │ 0° │ -90° │ 0° │ 0° │ 0° │
│ qn │ 0° │ 45° │ 180° │ 0° │ 45° │ 0° │
└─────┴─────┴──────┴───────┴─────┴──────┴─────┘Wyświetlona została tabela, w której zawarte są parametry DH, jak również limity \(q^-\) oraz \(q^+\) dla poszczególnych przegubów. W przypadku robota Puma560 mamy same przeguby obrotowe, więc zmienne q1…q6 są wyłącznie w kolumnie \(\theta_j\). Druga z wyświetlonych tabel przedstawia zdefiniowane specyficzne konfiguracje zmiennych:
- qz - konfiguracja zerowa, w której manipulator przypomina literę ‘L’,
- qr - ustawienie pionowe (ready),
- qs - ustawienie z ramieniem wyprostowanym w kierunku osi x (stretched out),
- qn - konfiguracja nominalna, nieosobliwa.
Lista zdefiniowanych konfiguracji i ich znaczenie zależy od modelu robota, można ją sprawdzić w dokumentacji.
Każdy obiekt klasy DHRobot przechowuje wiele informacji,
do których dostęp mamy za pomocą metod (lub atrybutów) tej klasy.
Poniżej kod wyświetlający niektóre informacje dotyczące wczytanego
robota.
robot = rtb.models.DH.Puma560()
# Sprawdzenie nazwy i producenta robota
print("Name: ", robot.name)
print("Manufacturer: ", robot.manufacturer)
# Sprawdzenie konfiguracji (rodzajów) przegubów (R - obrotowy, P - przesuwny)
print("Joint configuration: ", robot.structure)
# Sprawdzenie, które przeguby są obrotowe
print("Revolute joints: ", robot.revolutejoints)
# Sprawdzenie, które przeguby są przesuwne
print("Prismatic joints: ", robot.prismaticjoints)
# Sprawdzenie liczby węzłów
print("Number of joints: ", robot.n)
# Sprawdzenie czy manipulator jest opisany zmodyfikowaną notacją DH (1) lub standardową notacją DH (0)
print("MDH: ", robot.mdh)
# Sprawdzenie czy robot posiada nadgarstek sferyczny
print("Spherical wrist: ", robot.isspherical())
# Sprawdzenie maksymalnego zasięgu robota
print("Reach: ", robot.reach)
# Dodawanie własnej konfiguracji
robot.addconfiguration_attr("mycfg", [0.1, 0.2, 0.3, 0.4, 0.5, 0.6])
print(robot.mycfg)Zadanie:
Sprawdź powyższe informacje dla różnych modeli robotów.
Analogicznie możemy odczytać dane dotyczące poszczególnych połączeń
manipulatora - korzystamy tutaj z klasy DHLink. Przykład
dla przegubu pierwszego (indeks 0):
# Konfiguracja kinematyczna: 0 -> przegub obrotowy, 1 -> przesuwny
print(robot.links[0].sigma)
# Konwencja: 0 -> standardowa DH, 1 -> zmodyfikowana DH
print(robot.links[0].mdh)
# Sprawdzenie masy członu
print(robot.links[0].m)Robotics Toolbox umożliwia graficzne przedstawienie robota w
uproszczonej formie w wybranej konfiguracji. Służy do tego metoda
plot().
robot = rtb.models.DH.Puma560()
robot.plot(robot.qn, block = True, limits = None)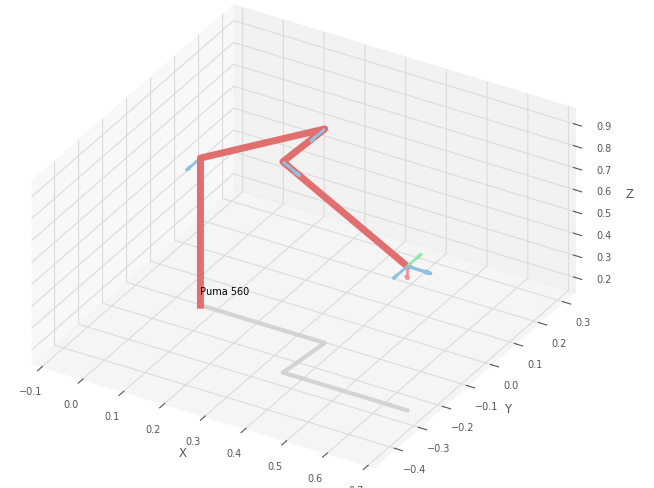
W sytuacji, gdy robot byłby mało widoczny, można wyskalować widok
zmieniając limity osi na rysunku (przykładowa zmiana: z
limits = None na
limits = [x_min, x_max, y_min, y_max, z_min, z_max], np.:
limits = [-1,1,-1,1,-1,1]).
Zadanie:
Dla kilku wybranych robotów wykonać wykresy w dostępnych domyślnie konfiguracjach q. Dodać jedną własną konfigurację i sprawdzić ustawienie robota na wykresie. Warto również wyszukać w sieci zdjęcia przedstawiające jak dany robot wygląda w rzeczywistości.
Istnieje również możliwość wykonania wykresu interaktywnego - umożliwiającego poruszanie poszczególnymi przegubami (tzw. funkcja teach pendant). Przykład:
robot = rtb.models.DH.Puma560()
robot.teach(robot.qr) # argument jest opcjonalny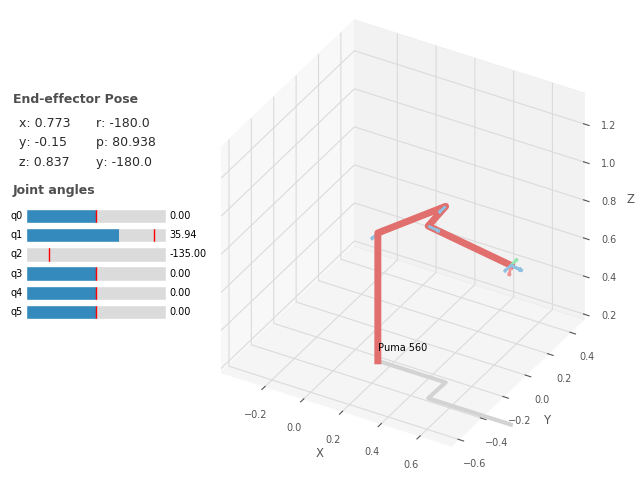
Dla funkcji teach istnieje taka sama możliwość
skalowania wykresu jak w przykładzie powyżej z plot.
Kinematyka prosta
Na powyższym rysunku oprócz suwaków służacych do zmiany wartości zmiennych konfiguracyjnych widzimy wartości opisujące położenie końcówki (x, y, z, roll, pitch, yaw). Zostały one wyznaczone dzięki rozwiązaniu zadania kinematyki prostej.
Przypomnienie:
Zadanie kinematyki prostej: zmienne konfiguracyjne \(q \rightarrow\) położenie końcówki \(\xi\)
\(\xi = F(q)\)
Wyznaczenie położenia końcówki (rozwiązanie zadania kinematyki
prostej) w Robotics Toolbox jest bardzo łatwe - służy do tego metoda
fkine(). Funkcja zwraca położenie końcówki
(SE3 - macierz 4x4) obliczoną na podstawie parametrów
członów i podanych jako argument wartości zmiennych konfiguracyjnych.
Przykład:
robot = rtb.models.DH.Puma560()
print(robot.q)
[0. 0. 0. 0. 0. 0.]
T = robot.fkine(robot.q)
print(T)
1 0 0 0.4521
0 1 0 -0.15
0 0 1 1.104
0 0 0 1
# lub
q_tmp = [0.5, 0., 0.9, 1.2, 0.2, 0.7]
T = robot.fkine(q_tmp)
print(T)
-0.7307 -0.2764 -0.6242 0.1651
0.6629 -0.5058 -0.552 -0.08078
-0.1631 -0.8172 0.5528 0.9561
0 0 0 1 W ten sposób wyznaczona została macierz transformacji pomiędzy bazą
robota a jego końcówką dla konkretnych wartości zmiennych q.
Dodatkowo można wprowadzić transformacje opisujące położenie układu bazy
oraz narzędzia (TCP - Tool Center Point). Służą do tego
atrybuty base oraz tool, które są obiektami klasy
SE3. Poniżej przykład, w którym TCP zostało przesunięte o 5
cm wzdłuż osi z układu T6 (ostatniego układu
współrzędnych robota). Analogicznie układ base jest
modyfikowany względem układu zerowego. Jak widać na poniższym
przykładzie, zmiana wartości tool i base powoduje
widoczne zmiany w wyniku kinematyki prostej.
print(robot.fkine(robot.q))
1 0 0 0.4521
0 1 0 -0.15
0 0 1 1.104
0 0 0 1
robot.tool = SE3(0, 0, 0.05)
print(robot.fkine(robot.q))
1 0 0 0.4521
0 1 0 -0.15
0 0 1 1.154
0 0 0 1 Zadanie:
Zmodyfikuj układ base w taki sposób, aby robot był “zawieszony na suficie”. Przyjmij wysokość sufitu równą 3 metry.
Istnieje również możliwość wyznaczenia transformacji dla różnych
zestawów wektora q. Aby to zrobić, należy podać jako argument
fkine nie pojedynczy wektor lecz macierz, której wiersze
stanowią kolejne wektory q. Wówczas wynikiem funkcji jest lista
transformacji.
W RTB można wyznaczyć kinematykę prostą nie tylko dla końcówki, ale
także dla poszczególnych układów. Metoda fkine_all()
pozwala na wyznaczenie transformacji pomiędzy układem odniesienia a
wszystkimi układami współrzędnych robota. Przykład:
q_tmp = [0.5, 0., 0.9, 1.2, 0.2, 0.7]
T = robot.fkine_all(q_tmp)
# wynikiem jest lista transformacji - jest ich tyle ile przegubów robota + 1 (układ bazy)
print(len(T))
7Kinematyka odwrotna
Pokazaliśmy w jaki sposób można wyznaczyć położenie końcówki na podstawie znajomości wartości współrzędnych konfiguracyjnych. Jednak z punktu widzenia praktycznego istotniejszy jest problem odwrotny: jakie ustawienie zmiennych konfiguracyjnych pozwoli na umieszczenie końcówki w zadanym położeniu? Na przykład znając położenie przedmiotu w przestrzeni kartezjańskiej (xyz) chcemy ustalić wartości kątów (i przesunięć) w przegubach, które pozwolą na chwycenie tego obiektu przez robota.
Przypomnienie:
Zadanie kinematyki odwrotnej: położenie końcówki \(\xi \rightarrow\) zmienne konfiguracyjne \(q\)
\(q = F^{-1}(\xi)\)
Do rozwiązania zadania kinematyki odwrotnej można zastosować dwa rodzaje metod. Pierwsze - analityczne - mogą opierać się o podejście algebraiczne lub geometryczne. Wadą metod analitycznych jest fakt, że wraz ze wzrostem liczby złącz robota wzrasta poziom trudności rozwiązania kinematyki odwrotnej. Alternatywę stanowią metody numeryczne (iteracyjne) oferujące rozwiązanie przybliżone.
Nadgarstek sferyczny to cecha znacznej większości współczesnych ramion robotycznych. Ten typ nadgarstka cechuje się trzema ortogonalnymi osiami przecinającymi się w tym samym punkcie (jest to mechanizm podobny do gimbala, posiada osobliwości). Położenie końcówki jest zdefiniowane przez układ w nadgarstku. Dowolną orientację końcówki roboczej uzyskuje się niezależnie za pomocą trzech przegubów nadgarstka. Ponieważ osie nadgarstka przecinają się w tym samym punkcie, powodują zerowe przesunięcie, a zatem pozycja końcówki jest funkcją zmiennych tylko trzech pierwszych przegubów. Jest to znaczne uproszczenie, które umożliwia znalezienie rozwiązania kinematyki odwrotnej w postaci jawnej (analitycznie) dla 6-osiowych manipulatorów.
Robotics Toolbox oferuje różne funkcje służące do rozwiązania zadania kinematyki odwrotnej:
| Metody analityczne | Metody numeryczne | |
|---|---|---|
| Python | ikine_a (tylko dla Puma560) |
ikine_LM, ikine_QP, ikine_GN,
ikine_NR |
| C++ Python wrappers | brak | ik_LM, ik_GN, ik_NR |
Przykład:
robot = rtb.models.DH.Puma560()
# print(robot.qn)
T = robot.fkine(robot.qn)
ik_solution = robot.ikine_a(T=T, config="rd") #konfiguracja right down
# print(ik_solution.q)
robot.plot(ik_solution.q, block = True)W powyższym przykładzie dla robota Puma w konfiguracji qn wyznaczono położenie końcówki (kinematyka prosta). Następnie obliczono kinematykę odwrotną dla tego położenia metodą analityczną (w RTB tylko model robota Puma560 ma zaimplementowaną metodę analityczną). Kinematyka odwrotna cechuje się tym, że może mieć wiele rozwiązań - niekiedy robot może osiągnąć to samo położenie końcówki ustawiając przeguby w różny sposób. W przykładzie powyżej wykonano wizualizacje robota w dwóch położeniach - najpierw robot znajduje się w konfiguracji qn, a następnie w konfiguracji wyznaczonej z kinematyki odwrotnej. Położenie końcówki w obu przypadkach jest taka sama, natomiast wartości zmiennych konfiguracyjnych są inne. Pierwsza konfiguracja jest nazywana “elbow up”, a druga “elbow down”. Jawne wskazanie docelowej konfiguracji jest możliwe tylko w metodach analitycznych, natomiast w metodach numerycznych efekt zależy jedynie od konfiguracji początkowej (wektora wartości początkowych q0).
Zadanie:
Uruchom przykładowy kod i spójrz na wizualizacje. Zastanów się samodzielnie, czy istnieją jeszcze inne rozwiązania (inne konfiguracje) dla tego samego położenia końcówki. Zmodyfikuj parametr config w funkcjiikine_ai sprawdź pozostałe możliwości.
Kinematyka prędkości - Jakobian
Kolejną cechą RTB jest możliwość wyznaczenia Jakobianu. Służą do tego
dwie metody klasy DHRobot: jacob0() oraz
jacobe().
Przypomnienie:
Jakobian \(J(q)\) opisuje zależność między prędkościami węzłowymi \(\dot{q}\) a prędkościami końcówki roboczej w układzie kartezjańskim xyz.
\(v=J(q)\dot{q}\)
gdzie \(v=(v_x,v_y,v_z,\omega_x,\omega_y,\omega_z)\) to wektor prędkości końcówki roboczej względem globalnego (bazowego) układu współrzędnych zawierający część reprezentującą prędkość liniową i obrotową. Jakobian ten jest nazywany Jakobianem geometrycznym lub Jakobianem manipulatora.
Do wyznaczenia Jakobianu opisującego prędkość końcówki względem
układu globalnego (bazowego) służy funkcja jacob0.
Natomiast funkcja jacobe wyznacza Jakobian opisujący
prędkość końcówki w układzie końcówki (end-effector).
Przykład:
robot = rtb.models.DH.Puma560()
# aktualny wektor wspolrzednych konfiguracyjnych
print(robot.q)
[0. 0. 0. 0. 0. 0.]
# względem układu globalnego (bazowego)
J = robot.jacob0(robot.q)
# wyświetlanie numpy.ndarray z określoną precyzją i bez notacji naukowej:
np.set_printoptions(precision=3, suppress=True)
print(J)
[[ 0.15 -0.432 -0.432 0. 0. 0. ]
[ 0.452 0. 0. 0. 0. 0. ]
[ 0. 0.452 0.02 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. ]
[ 0. -1. -1. 0. -1. 0. ]
[ 1. 0. 0. 1. 0. 1. ]]
q_tmp = [0.5, 0., 0.9, 1.2, 0.2, 0.7]
J = robot.jacob0(q_tmp)
print(J)
[[ 0.081 -0.25 -0.25 0. 0. 0. ]
[ 0.165 -0.136 -0.136 0. 0. 0. ]
[ 0. 0.106 -0.326 0. 0. 0. ]
[ 0. 0.479 0.479 -0.687 0.682 -0.624]
[ 0. -0.878 -0.878 -0.376 -0.04 -0.552]
[ 1. -0. -0. 0.622 0.73 0.553]]
# względem układu końcówki (end-effector)
Je = robot.jacobe(q_tmp)
print(Je)
[[ 0.05 0.075 0.145 0. 0. 0. ]
[-0.106 0.051 0.404 0. 0. 0. ]
[-0.142 0.29 0.051 0. 0. 0. ]
[-0.163 -0.932 -0.932 0.152 -0.644 0. ]
[-0.817 0.311 0.311 -0.128 -0.765 0. ]
[ 0.553 0.185 0.185 0.98 0. 1. ]]Zadanie:
Uruchom ten sam przykład dla robota Panda. Zwróć uwagę na wymiary uzyskanego Jakobianu i zastanów się z czego one wynikają.
🔥 💥 Zadania do wykonania: 💥 🔥
Zadanie 1.
Dany jest robot przedstawiony na rysunku wraz z opisem w standardowej
notacji Denavita-Hartenberga (tabela). Na podstawie tabeli zdefiniuj
robota przy użyciu klasy DHRobot, w tym celu:
- Wykorzystaj zmienne symboliczne (funkcję
symbol) do reprezentacji wymiarów \(l_1\) i \(l_2\). Liczbę \(\pi\) (\(\pi/2=90^\circ\)) również przedstaw w symbolicznej formie, poszukaj do tego dedykowanej funkcji. - Sprawdź w jaki sposób należy uwzględnić dodatkowe wartości
pojawiające się przy zmiennych konfiguracyjnych w tabeli (\(\theta_2\boldsymbol{+90^\circ}\) oraz \(\boldsymbol{l_2}+d_3\)), wykorzystaj
odpowiedni parametr konstruktora klasy
DHLink(RevoluteDH,PrismaticDH). - Wyświetl zdefiniowaną tabelę i sprawdź poprawność z tabelą daną w zadaniu.
Uwaga: funkcja
print(robot)może zwrócić błędy, gdy używamy zmiennych symbolicznych. W zamian można trzykrotnie użyć funkcjiprint(robot.links[i]), gdzie i to nr przegubu (od 0 do 2 w tym przypadku).
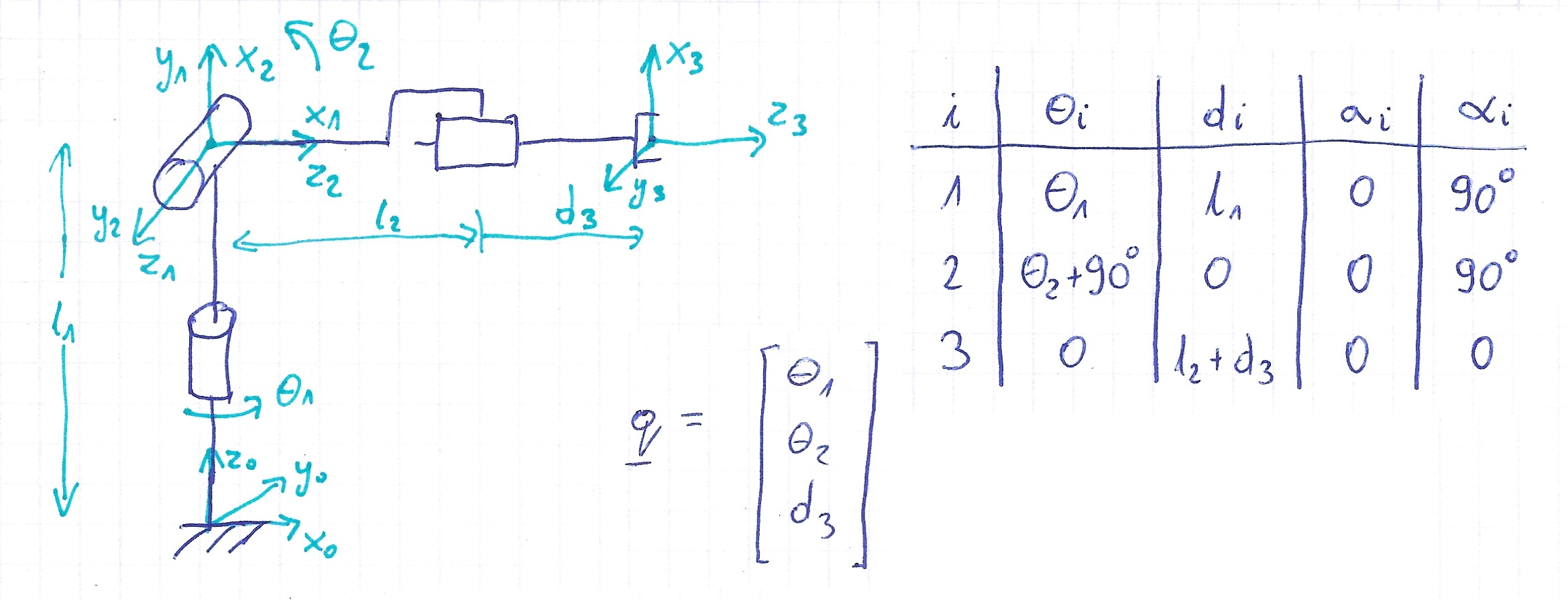
Zadanie 2.
Dla zdefiniowanego w zadaniu 1. robota rozwiązać zadanie
kinematyki prostej korzystając z funkcji
fkine. Jako argument funkcji podać zmienne symboliczne.
Zweryfikować poprawność uzyskanej transformacji. Prawidłowe
rozwiązanie:
\(T_3^0=\begin{bmatrix} -c_1s_2 & s_1
& c_1c_2 & c_1c_2(l_2+d_3)\\ -s_1s_2 & -c_1 & s_1c_2
& s_1c_2(l_2+d_3)\\ c_2 & 0 & s_2 & s_2(l_2+d_3)+l_1\\ 0
& 0 & 0 & 1 \end{bmatrix}\)
gdzie \(s_1 = sin(\theta_1)\), \(c_1 = cos(\theta_1)\), \(s_2 = sin(\theta_2)\), \(c_2 = cos(\theta_2)\)
Zadanie 3.
Dla zdefiniowanego w zadaniu 1. robota wyznaczyć
jakobian opisujący prędkość liniową i obrotową końcówki
względem układu globalnego. Jako argument funkcji podać zmienne
symboliczne. Jeśli wyświetlany wynik nie jest uproszczony (tzn.
pojawiają się takie wyrażenia jak jedynka trygonometryczna), to poszukaj
funkcji
umożliwiającej jego uproszczenie. Zweryfikować poprawność uzyskanej
transformacji. Prawidłowe rozwiązanie:
\(J=\begin{bmatrix} -s_1c_2(l_2+d_3) &
-c_1s_2(l_2+d_3) & c_1c_2\\ c_1c_2(l_2+d_3) & -s_1s_2(l_2+d_3)
& s_1c_2\\ 0 & c_2(l_2+d_3) & s_2\\ 0 & s_1 & 0\\ 0
& -c_1 & 0\\ 1 & 0 & 0 \end{bmatrix}\)
gdzie \(s_1 = sin(\theta_1)\), \(c_1 = cos(\theta_1)\), \(s_2 = sin(\theta_2)\), \(c_2 = cos(\theta_2)\)
Zadanie 4.
Ponownie zdefiniuj robota z zadania 1. za pomocą klasy
DHRobot, tym razem zamiast zmiennych symbolicznych
wykorzystaj wartości stałe: \(\) (skorzystaj z np.pi lub
math.pi), \(l_1=1\), \(l_2=0.4\).
Rozwiąż kinematykę prostą dla \(q=[0.1 \;\; 1 \;\; 0.4]\) Dla otrzymanej
transformacji wyznacz kinematykę odwrotną i sprawdź, czy wynik jest
równy \(q\).
Korzystając z przegubów pryzmatycznych roboticstoolbox wymaga podania limitów dla przesunięcia. Dlatego wewnątrz konstruktora
PrismaticDHdodaj argumentqlim=[0,3]
Zadanie 5.
Dla robota Puma560 porównaj czasy oraz
błędy rozwiązywania zadania kinematyki odwrotnej
różnymi metodami: ikine_a, ikine_LM,
ikine_QP, ikine_GN, ikine_NR.
Jako argument funkcji ikine wykorzystaj położenie końcówki
T dla konfiguracji qn.
Dla porównania metod należy wyznaczyć błąd samodzielnie - jako różnicę
(normę) pomiędzy położeniem końcówki T a położeniem uzyskanym
po wyznaczeniu kinematyki prostej z konfiguracji otrzymanej w wyniku
kinematyki odwrotnej.
Która metoda jest w tym przypadku najszybsza i która cechuje się najmniejszym błędem?
Zadanie domowe
W ramach lab nr 2 należy rozwiązać zadanie domowe (zadanie 3. i 5. z instrukcji) na eKursie (ma ono formę zadania testowego w CodeRunnerze). Termin wykonania jest wyświetlony w module zadania na eKursie.