Modelowanie i sterowanie robotów - laboratorium

Lab 3 - Metody planowania trajektorii ruchu manipulatorów w RT

Politechnika Poznańska

Instytut Robotyki i Inteligencji Maszynowej

Jakub Chudziński, Bartłomiej Kulecki

Szablon kodu

Można skorzystać z następującego szablonu pliku .py:

# wczytanie potrzebnych podczas zajęć bibliotek:
import numpy as np
from spatialmath import *
import roboticstoolbox as rtb
from roboticstoolbox.tools.trajectory import *
from roboticstoolbox.backends.swift import Swift
import time
# ...

# definicje funkcji:
def przyklad_1():
    pass # zastąp tę linię swoim kodem

def zadanie_1():
    pass # zastąp tę linię swoim kodem
    
def zadanie_2():
    pass # zastąp tę linię swoim kodem

def zadanie_3():
    pass # zastąp tę linię swoim kodem

# ...

# wykonywanie wybranej funkcji
if __name__ == '__main__':
    przyklad_1()
    #...
    #zadanie_1()
    #zadanie_2()
    #zadanie_3()

Wstęp

W robotyce często spotykamy się z generowaniem licznych zadanych położeń, które cechują się płynnym charakterem zmian w czasie, zarówno w translacji, jak i w rotacji. Ścieżka jest to pewien konstrukt przestrzenny - lista miejsc w przestrzeni, które prowadzą od położenia początkowego do końcowego. Natomiast trajektoria to ścieżka o określonym czasie. Na przykład istnieje ścieżka z A do B, ale istnieje trajektoria z A do B w czasie 10 sekund lub przy prędkości \(2\). Ważną cechą trajektorii jest to, że jest płynna - pozycja i orientacja zmieniają się płynnie w czasie. Rozważmy najpierw sposób generowania płynnych trajektorii w jednym wymiarze. Następnie rozszerzymy to na przypadek wielowymiarowy, a następnie na odcinkowo-liniowe trajektorie, które odwiedzają wiele punktów pośrednich bez zatrzymywania się.

Trajektoria jednowymiarowa

Ważnym aspektem trajektorii jednowymiarowej jako skalarnej funkcji czasu jest płynność. Oznacza to w praktyce, że chcemy aby pierwsze pochodne tej funkcji były ciągłe. Zazwyczaj wymagana jest ciągłość pierwszej i drugiej pochodnej, czyli prędkości i przyspieszenia. Dobrym kandydatem do uzyskania płynnej trajektorii jest funkcja wielomianowa. Zazwyczaj wykorzystywane są wielomiany 5-tego stopnia: \[s(t)=At^5+Bt^4+Ct^3+Dt^2+Et+F\] gdzie czas \(t\), natomiast pierwsza i druga pochodna:
\((t)=5At^4+4Bt3+3Ct^2+2Dt+E\)
\((t)=20At^3+12Bt2+6Ct+2D\)

W Robotics Toolbox jednowymiarową trajektorię wielomianową można wygenerować dzięki funkcji quintic. Poniżej przykład stworzenia trajektorii składającej się z 50 próbek o wartościach położenia w zakresie od 0 do 1. Trajektoria jest rysowana na 3 wykresach: pozycja, prędkość, przyspieszenie. Dla trajektorii oznaczonej literą a) pozostawiono domyślne wartości prędkości początkowej i końcowej równe zero. W drugim przypadku ustawiono prędkość początkową na 0,5.

Narysujmy przebiegi trajektorii:

# wykres a)
traj = quintic(0, 1, 50) # trajektoria w zakresie od 0 do 1 z 50 próbek
traj.plot(traj)

# wykres b)
traj = quintic(0, 1, 50, 0.5) # trajektoria z niezerową prędkością początkową
traj.plot(traj)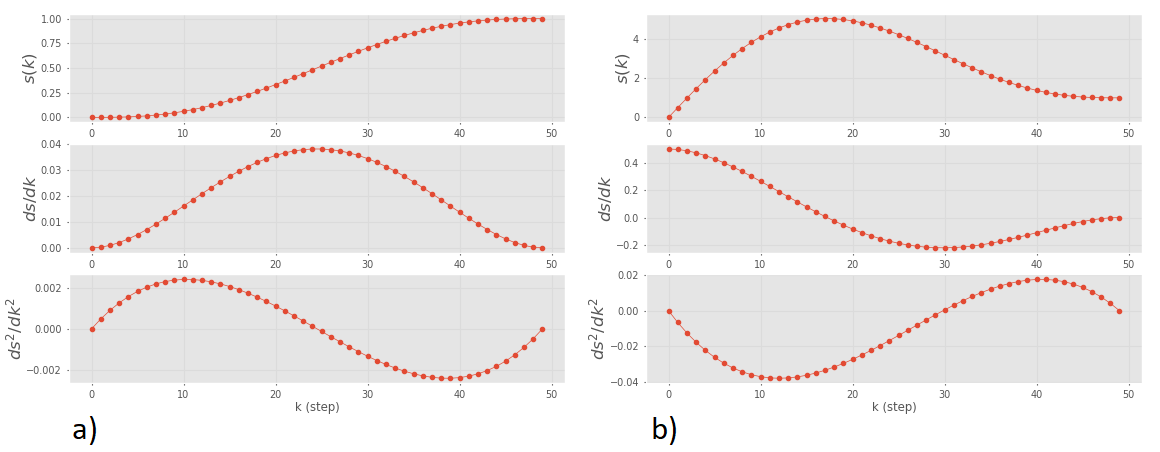

Wyniki przedstawione na rys. b) ilustrują ważny problem z trajektorią wielomianową. Niezerowa prędkość początkowa powoduje, że położenie (pierwszy wykres od góry) przekracza wartość końcową - osiąga wartość szczytową równą 5 dla zadanej trajektorii mieszczącej się w zakresie od 0 do 1. Kolejny praktyczny problem z wielomianami widoczny jest na środkowym wykresie na rys. a). Prędkość osiąga wartość szczytową przy k = 25, co oznacza, że przez większość czasu prędkość jest znacznie mniejsza niż maksymalna. W tym przypadku średnia prędkość to tylko około 52% wartości szczytowej, więc można stwierdzić, że nie używamy napędu w pełni jego możliwości. Prawdziwy przegub robota ma precyzyjnie określony zakres prędkości i celem algorytmu sterowania jest zapewnienie, aby ruch był wykonywany z maksymalną prędkością przez jak najdłuższy okres czasu, minimalizując przy tym całkowity czas ruchu. Chcielibyśmy więc, aby krzywa prędkości była spłaszczona u góry.

Dobrą alternatywą jest trajektoria hybrydowa, która ma segment o stałej prędkości oraz segmenty wielomianowe przy przyspieszaniu i zwalnianiu. W RTB wystarczy użyć funkcji trapezoidal. Oto trajektoria hybrydowa dla tego samego przykładu co wyżej:

traj = trapezoidal(0, 1, 50)
traj.plot(traj)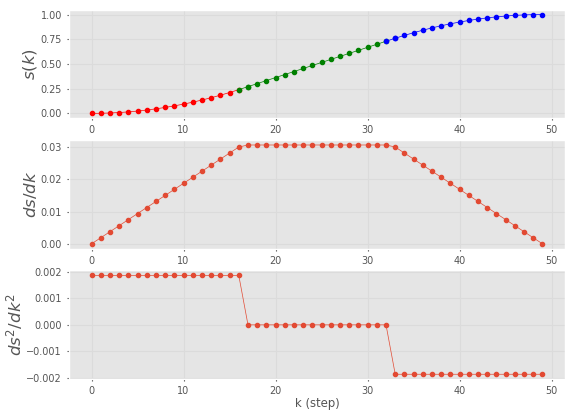

Trajektoria tego typu jest nazywana trajektorią trapezoidalną - ze względu na profil prędkości. Jest ona często stosowana dla napędów robotów przemysłowych.

Dokonaj krótkiej analizy
Spójrz na wykres przyspieszeń w przypadku trajektorii trapezoidalnej i porównaj go z przebiegiem dla trajektorii wielomianowej. Jaki charakter mają przebiegi podczas rozpędzania i hamowania, czy w obu przypadkach są płynne? Do czego mogłoby prowadzić zadawanie krótkich ruchów z ogromną prędkością następujących po sobie? - w ruchu wystąpiłyby szarpnięcia.

Wartości pozycji, prędkości i przyspieszenia są dostępne jako atrybuty obiektu typu trajectory (w przykładzie jest to zmienna traj) - q, qd, qdd.

Funkcja trapezoidal automatycznie dobrała wartość prędkości na odcinku liniowym, jest ona równa:

print(max(traj.qd))
    0.030612

Wartość tę można również ustalić ręcznie, wystarczy podać ją jako czwarty argument funkcji trapezoidal. >Zadanie:
>Sprawdź, jak będzie wyglądał wykres dla prędkości na odcinku liniowym o mniejszej i większej wartości od prędkości nominalnej. Zastanów się, czy w praktyce wartość tę można ustalić dowolnie i jakie są ewentualne ograniczenia.

W dalszej części rozpatrzymy trajektorie wielowymiarowe. ___ ### Trajektoria w przestrzeni konfiguracyjnej Roboty zazwyczaj posiadają więcej niż jedną oś ruchu, więc trajektoria jednowymiarowa jest dla nich niewystarczająca. Najpopularniejsze są roboty o 6 stopniach swobody, czyli 6 osiach ruchu, a co za tym idzie 6 zmiennych konfiguracyjnych. Chcąc zaplanować trajektorię ruchu takiego robota musimy zatem wyznaczyć trajektorię dla każdej osi. Rozważmy najpierw przykład robota o dwóch osiach, wektor zmiennych konfiguracyjnych \(q=[q_1 \;\; q_2]\). Załóżmy, że chcemy przemieścić się pomiędzy dwoma konfiguracjami (początkową i końcową) - od (0, 2) do (1, −1). Aby wyznaczyć trajektorię w Robotics Toolbox, można użyć funkcji: - jtraj - generuje trajektorię wielomianową dla wszystkich zmiennych, - mtraj - generuje trajektorię wielomianową lub trapezoidalną.

Przykład:

# trajektoria wielomianowa
traj = jtraj([0, 2], [1, -1], 50)
traj.plot(traj)
# lub
traj = mtraj(quintic, [0, 2], [1, -1], 50)
traj.plot(traj)

# trajektoria trapezoidalna
traj = mtraj(trapezoidal, [0, 2], [1, -1], 50)
traj.plot(traj)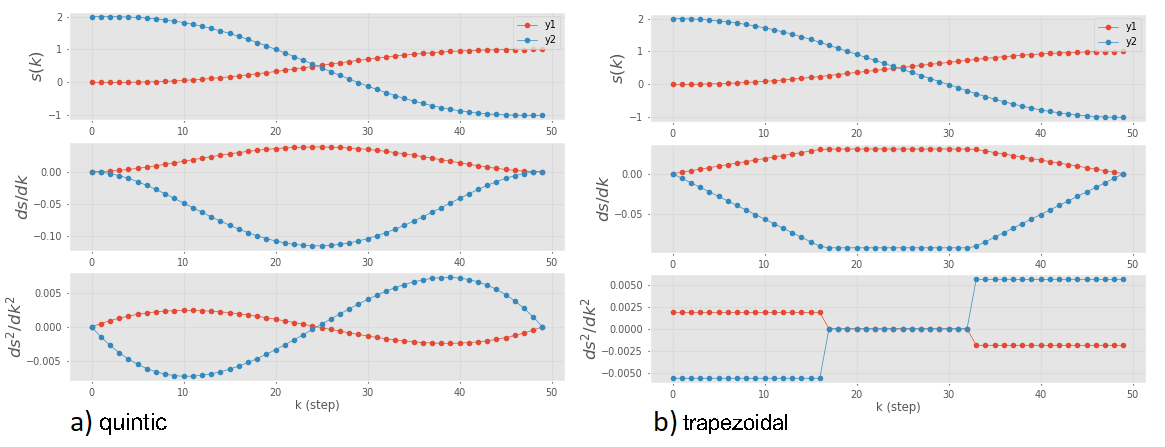

Analogicznie możemy zaplanować trajektorię dla robota podając dwie konfiguracje, pomiędzy którymi ma być zaplanowana trajektoria, np.

robot = rtb.models.DH.Panda()
traj = jtraj(robot.qz, robot.qr, 50)
traj.plot(traj)

# lub
traj = mtraj(quintic, robot.qz, robot.qr, 50)
traj.plot(traj)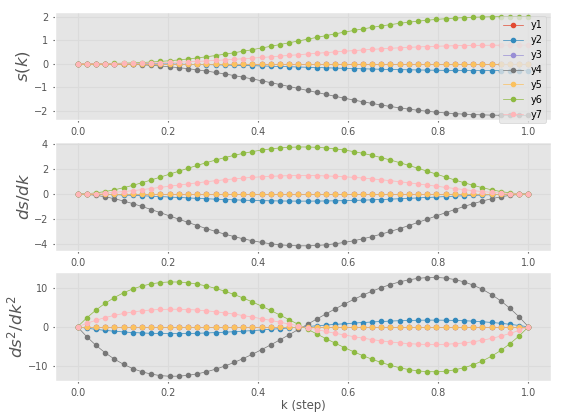

Trajektoria o wielu odcinkach

W robotyce często wymagane jest zaplanowanie trajektorii pomiędzy punktem początkowym a końcowym, która będzie przechodzić przez jeden lub więcej punktów pośrednich bez zatrzymywania. Przykładem może być np. proces spawania, podczas którego robot wykonuje fragmentami ruch liniowy lub ruch z unikaniem kolizji z przeszkodami. Ilustrację tego typu trajektorii przedstawiono poniżej na jednowymiarowym przykładzie. Trajektoria we współrzędnych konfiguracyjnych prowadzi od punktu \(q_1\) do \(q_4\) przez dwa punkty pośrednie (tzw. via points) \(q_2\) i \(q_3\). W Robotics Toolbox tego typu trajektorię można stworzyć dzięki funkcji mstraj.

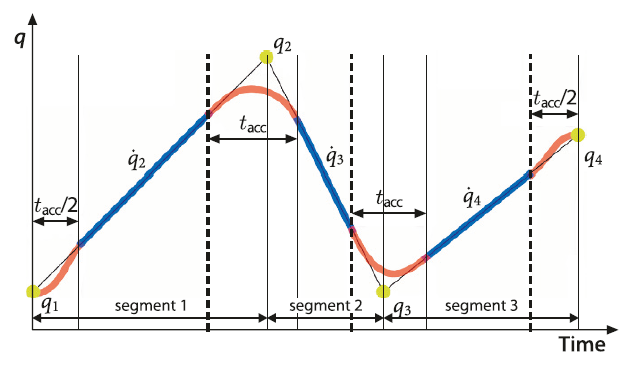Przykład jednowymiarowej trajektorii typu mstraj [1]

# Przykład dla robota o 2 stopniach swobody, trajektoria składa się z 4 punktów
via_pt = np.array([[0,0], [1,0.5], [0.2,2], [0.5,1]])
traj = mstraj(via_pt, dt=0.02, tacc=0.2, qdmax=2.0)
rtb.xplot(traj.q, block=True)

Trajektoria w przestrzeni kartezjańskiej

Inną istotną kwestią w analizowanym podczas tego laboratorium temacie jest generowanie płynnej trajektorii pomiędzy dwoma położeniami w układzie kartezjańskim 3D, czyli pomiędzy dwoma położeniami należącymi do SE(3). W robotyce często nazywa się to ruchem kartezjańskim.

Ważnym zagadnieniem jest tutaj interpolacja orientacji. Wymagane jest, aby zmiana orientacji końcówki robota podczas ruchu była płynna. Interpolacja liniowa macierzy rotacji nie jest tutaj dobrym rozwiązaniem, ponieważ macierze wynikowe zwykle nie będą spełniały warunku ortonormalności.

Inna reprezentacja rotacji to 3 kąty Eulera lub kąty roll, pitch, yaw. Rozwiązaniem może być więc następujące postępowanie: konwersja macierzy rotacji do 3 kątów, interpolacja liniowa kątów, wyznaczenie macierzy rotacji. Ta metoda ma jednak swoje wady. Można zauważyć, że podczas ruchu, dla dużych wartości kątów obrotów, oś wokół której następuje obrót jest zmienna (ruch jest w pewnym sensie nieskoordynowany). Poza tym problemem są osobliwości. Gdy ruch ma miejsce w pobliżu konfiguracji osobliwych, następuje gwałtowny wzrost prędkości np. jednego z kątów.

Rozwiązaniem powyższych problemów jest interpolacja orientacji przy użyciu kwaternionów. Zmianę orientacji zdefiniowaną w ten sposób cechuje obrót wokół nieruchomej osi, dzięki czemu ruch jest wyraźnie płynniejszy.

Porównanie obu sposobów przedstawiono na animacjach poniżej. Widać tutaj zaletę interpolacji orientacji jako kwaternionów. Możemy sobie wyobrazić, że zwizualizowany sześcian jest wpisany w sferę (wierzchołki sześcianu leżą wtedy na powierzchni sfery). W przypadku kwaternionów wszystkie wierzchołki poruszają się w trakcie obrotu po powierzchni sfery. Ruch ten jest zazwyczaj wykonywany po najkrótszej możliwej drodze, która biegnie wzdłuż tzw. wielkiego koła (które stanowi przekrój sfery przechodzący przez jej środek).

interpolacja kątów RPY	interpolacja kwaternionu

Do generowania trajektorii w przestrzeni kartezjańskiej w Robotics Toolbox służy funkcja ctraj. Tworzy ona trajektorię pomiędzy dwoma położeniami SE3 (funkcja zwraca listę obiektów typu SE3). Aby zapewnić płynność, interpolacja orientacji jest zrealizowana na kwaternionach. Przykład wygenerowania trajektorii składającej się z 50 punktów pomiędzy dwoma położeniami (T1, T2):

T1 = SE3(0.4, 0.2, 0) * SE3.RPY([0, 0, 3])
T2 = SE3(-0.4, -0.2, 0.3) * SE3.RPY([-np.pi / 4, np.pi / 4, -np.pi / 2])
cart_traj = ctraj(T1, T2, 50)
print(cart_traj)

Wizualizacja ruchu robota w Robotics Toolbox

Pakiet Roboics Toolbox pozwala na animację robota z wykorzystaniem zewnętrznych narzędzi takich jak PyPlot (matplotlib) oraz Swift. Zainstalowaliśmy te narzędzia na pierwszych zajęciach (komendą z instrukcji nr 1). Poniżej przykład wizualizacji tej samej trajektorii w różnych środowiskach. Aby wygenerować trajektorię, ustalono położenie docelowe i orientację (OA) dla końcówki robota i wyznaczono kinematykę odwrotną dla tego położenia. Następnie skorzystano z funkcji jtraj do wygenerowania trajektorii pomiędzy konfiguracją zerową qz a konfiguracją otrzymaną z kinematyki odwrotnej.

Dla środowiska PyPlot i Swift wystarczy zastosować funkcję robot.plot() i jako argument podać trajektorię oraz nazwę backendu. Analogicznie jest w przypadku wizualizacji robota w pojedynczej konfiguracji bez ruchu (wtedy jako argument plot możemy podać np. robot.qz). Aby wykorzystać PyPlot najlepiej załadować robota z rtb.models.DH:

# PyPlot  
robot = rtb.models.DH.Panda()
T = SE3(0.7, 0.2, 0.1) * SE3.OA([0, 1, 0], [0, 0, -1])
solution = robot.ikine_LM(T)
traj = jtraj(robot.qz, solution.q, 50)
robot.plot(traj.q, backend = 'pyplot', limits=[-0.25, 1.25, -0.5, 0.5, 0, 1], movie='panda_pyplot.gif')

Natomiast dla wizualizacji ze Swiftem z rtb.models:

# Swift
robot = rtb.models.Panda()
T = SE3(0.7, 0.2, 0.1) * SE3.OA([0, 1, 0], [0, 0, -1])
solution = robot.ikine_LM(T)
traj = jtraj(robot.qz, solution.q, 50)
robot.plot(traj.q, backend = 'swift', loop=True)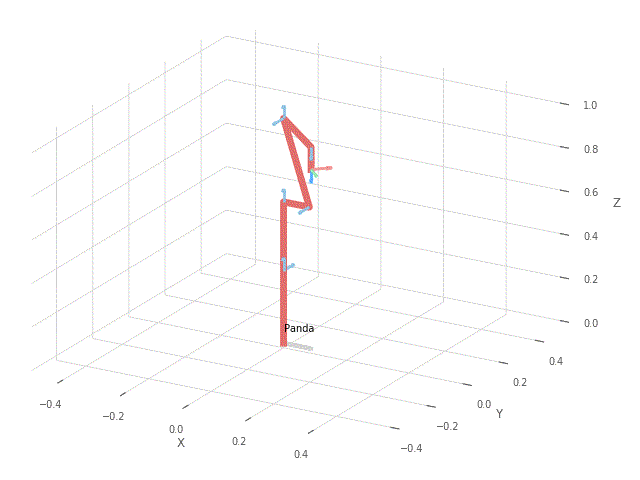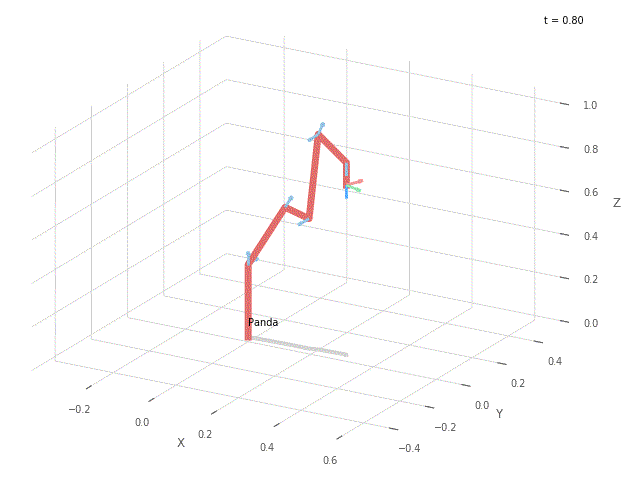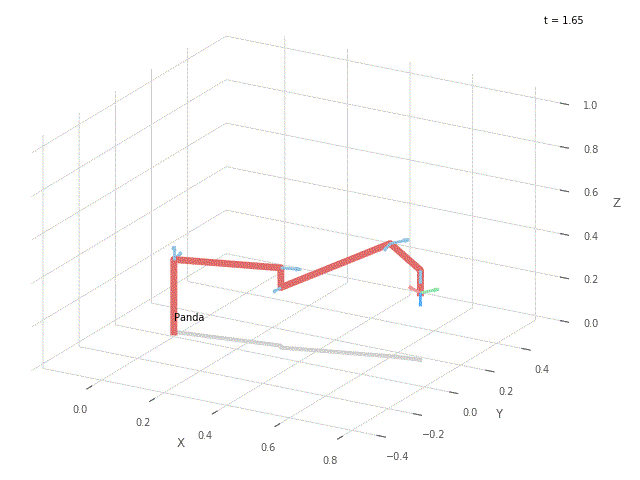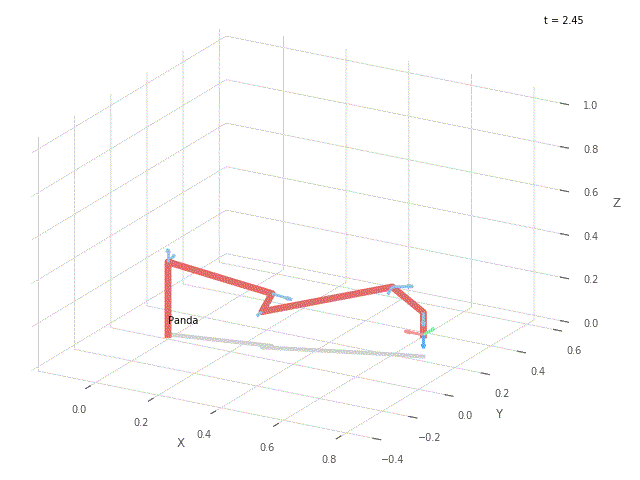

PyPlot	Swift

elif self.path.startswith("/retrieve/"):
    # print(f"Retrieving file: {self.path[10:]}")
    self.path = urllib.parse.unquote(self.path[9:])
    self.send_file_via_real_path()
    return

elif self.path.startswith("/retrieve/"):
    # print(f"Retrieving file: {self.path[10:]}")
    self.path = urllib.parse.unquote(self.path[10:])
    self.send_file_via_real_path()
    return

`env.launch(name=self.name + " Trajectory Plot", limits=limits, fig=fig)`

na:

`env.launch(name=self.name + " Trajectory Plot", limits=limits, fig=fig, realtime=True)`

Resolved Rate Motion Control (RRMC)

Prostym i eleganckim algorytmem, który pozwala na wygenerowanie prostoliniowej trajektorii pomiędzy dwoma położeniami w przestrzeni xyz jest RRMC. Algorytm ten nie wymaga obliczania kinematyki odwrotnej. Opiera się on na rzutowaniu prędkości liniowych i obrotowych końcówki \(v\) na prędkości “węzłowe” \(\). Wykorzystuje się do tego Jakobian: \[\dot{q}=J(q)^{-1}\cdot v\]

Pożądane prędkości \(v\) wyznacza się przy pomocy klasycznego regulatora typu P. W Robotics Toolbox dostępna jest funkcja rtb.p_servo, która jako argumenty przyjmuje dwa położenia (aktualne - \(T_{actual}\) i docelowe - \(T_{desired}\)) w układzie xyz i korzystając ze wzmocnienia \(k\) regulatora wyznacza prędkości we wszystkich osiach. Następnie korzystając z powyższego równania wyznaczane są prędkości dla zmiennych konfiguracyjnych (które można ustawić korzystając z robot.qd). Poprzedni wzór można zapisać zatem jako: \[\dot{q}=J(q)^{-1}\cdot k\cdot(T_{desired}-T_{actual})\] Należy jednak pamiętać, że warunkiem odwracalności jakobianu jest jego pełny rząd. Sytuacja, w której rząd manipulatora jest niepełny, ma miejsce, gdy manipulator jest redundantny lub znajduje się w konfiguracji osobliwej. Wówczas należy stosować pseudoodwrotność. Wielokrotne wyznaczanie jakobianu i jego pseudoodwrotności (w każdym kroku działania algorytmu) jest niewątpliwie wadą algorytmu RRMC. Poniżej przykład generowania ruchu pomiędzy dwoma położeniami za pomocą algorytmu RRMC:

# Make and instance of the Swift simulator and open it
env = Swift()
env.launch(realtime=True)

# Make a robot model and set its joint angles to the ready joint configuration
robot = rtb.models.Panda()
robot.q = robot.qr

# Set a desired and effector pose an an offset from the current end-effector pose
Tep = robot.fkine(robot.q) * SE3.Tx(0.2) * SE3.Ty(0.2) * SE3.Tz(0.45)

# Add the robot to the simulator
env.add(robot)
time.sleep(2)

# Simulate the robot while it has not arrived at the goal
arrived = False
while not arrived:
    # Work out the required end-effector velocity to go towards the goal
    v, arrived = rtb.p_servo(robot.fkine(robot.q), Tep, 1)

    # Set the robot's joint velocities (calculate pseudoinverse(J) * v)
    robot.qd = np.linalg.pinv(robot.jacobe(robot.q)) @ v

    # Step the simulator by 5 milliseconds
    env.step(0.005)

Zadanie:
Przetestuj algorytm RRMC z powyższego przykładu dla różnych położeń docelowych. Uwzględnij również zmianę orientacji.

🔥 💥 Zadania do wykonania: 💥 🔥

Zadanie 1.
Załaduj robota Puma560 (rtb.models.Puma560()) i wyświetl go w Swifcie w konfiguracji qz. Wyznacz położenie końcówki T_start dla początkowej konfiguracji qz. Następnie wyznacz różne położenia T_end: - przesuniętą o 20 cm w przód (wzdłuż globalnej osi x), - przesuniętą o 20 cm w lewo (wzdłuż globalnej osi y), - przesuniętą o 20 cm w górę (wzdłuż globalnej osi z). - przesuniętą o 25 cm w przód i obróconą tak, aby oś z końcówki była skierowana w przód, - przesuniętą o 20 cm w dół i obróconą tak, aby oś z końcówki była skierowana w lewo.

Dla wyznaczonego położenia T_end wyznacz kinematykę odwrotną. Wyznacz trajektorię jtraj pomiędzy konfiguracjami dla T_start i T_end. Dla każdego z wymienionych przesunięć (i obrotów) wykonaj osobną animację ruchu robota w Swifcie.

Zadanie 2.
Analogicznie jak w zadaniu 1, dla robota Puma560 wyznacz położenie końcówki T_start w konfiguracji qz. Następnie wyznacz położenie T_end: - przesuniętą o 30 cm w przód, 30 cm w dół i obróconą tak, aby oś z końcówki była skierowana w prawo.

Dla wyznaczonego położenia T_end wyznacz kinematykę odwrotną. Wyznacz trajektorię mtraj (z wykorzystaniem trapezoidal) pomiędzy konfiguracjami dla T_start i T_end. Wykonaj animację ruchu robota w Swifcie. Stwórz wykresy pozycji, prędkości i przyspieszenia dla wszystkich przegubów i porównaj je z wykresem uzyskanym dla jtraj dla tych samych położeń T_start, T_end.

Zadanie 3.
Napisz program, który za pomocą funkcji mstraj stworzy trajektorię dla robota Panda (o 7 stopniach swobody). Trajektoria ma rozpoczynać się od konfiguracji zerowej qz, po czym robot ma “narysować” okrąg w płaszczyźnie xy. Dane opisujące trajektorię:
- wysokość końcówki (podczas rysowania okręgu) = 0.15 - pozycja środka okręgu: x = 0.65, y = 0.2 - promień okręgu = 0.1

Wykonaj wykres przedstawiający punkty okręgu na płaszczyźnie xy. Stwórz wykres przedstawiający wartości kątów poszczególnych osi robota w czasie ruchu. Stwórz animację w wybranym środowisku (PyPlot / Swift), która pokaże realizację całej trajektorii przez robota Panda. Przykładowo:

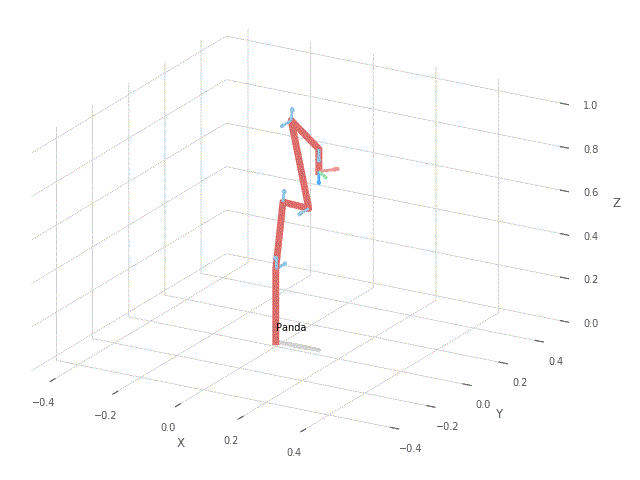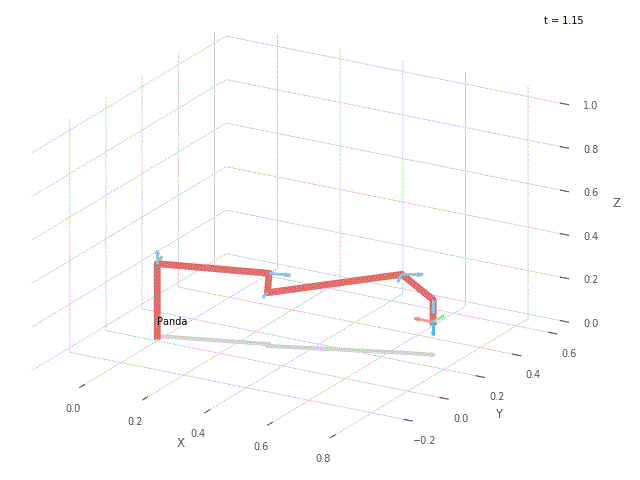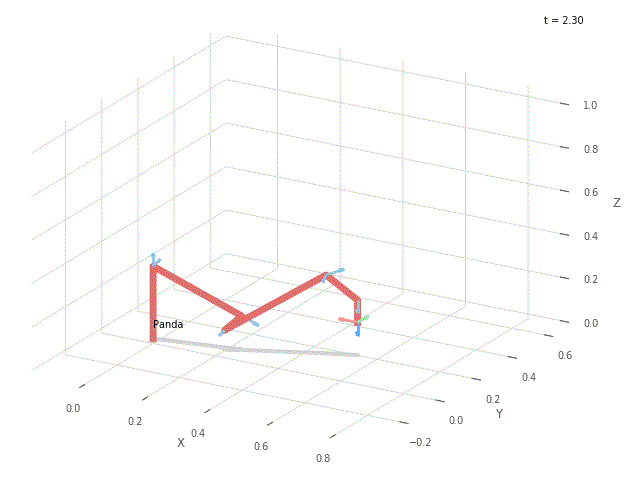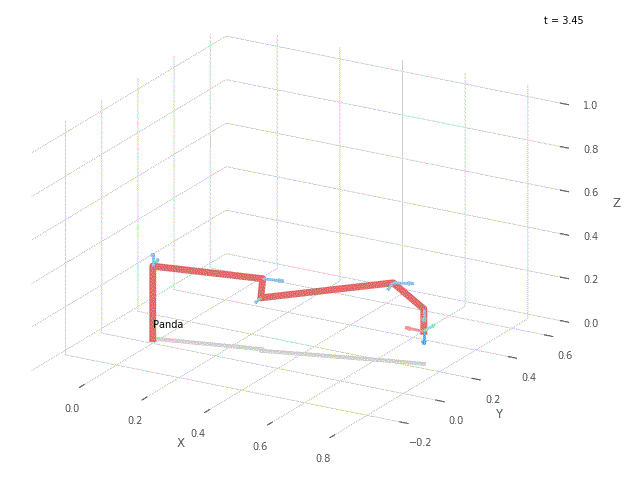Zadanie domowe

W ramach lab nr 3 należy wgrać na eKurs rozwiązanie zadania 3 - plik py zawierający kod oraz animację w formacie gif. Czas na oddanie jest wyświetlony w module zadania na eKursie.

Bibliografia

[1] Robotics, Vision & Control, Sec 3.3.3, Peter Corke, Springer 2017